¡Hola Indexados!
Uno de los temas mas importantes al entrar al mundo de las inversiones es calcular cuanto voy ganando o perdiendo, a través del tiempo. Sin embargo, es uno de los temas que menos se habla, tanto en YouTube e incluso blogs de finanzas. Esto genera que los nuevos inversores (e incluso antiguos) utilicen diversas formas de medir la rentabilidad de sus inversiones, algunos de manera correcta y otros de manera incorrecta.
Es por ello que, te traigo una guía completa para conocer todo el panorama con respecto a como calcular la rentabilidad de nuestras inversiones, pero antes, empecemos por lo primero: ¿Qué es la rentabilidad?.
¿Qué es la rentabilidad?
La rentabilidad es un indicador que mide en porcentaje (%) el resultado (beneficio) que se ha obtenido de una inversión inicial. Mide cuanto se ha incrementado este esfuerzo inicial para haber llegado a ese resultado final.
Ya entrando en el terreno de las inversiones, existen básicamente tres formas de obtener beneficios, lo que harán rentabilizar nuestras inversiones:
- Intereses: El mas conocido de todos. En las cuentas de ahorro o depósitos a plazo, se contratan estos productos financieros sabiendo de antemano cuanto se ganará (intereses). En donde, el capital inicial y los aportes que se realizaran constituyen la inversión inicial, y los intereses, el beneficio o resultado obtenido. Tu ganas de acuerdo al % interés pactado.
- Revalorización del capital: En la bolsa de valores, si yo adquiero una acción, bono, ETF, fondo mutuo, etc a un valor X (inversión inicial) y luego de un tiempo lo vendo a un mayor precio de lo que me costó, pues esa ganancia seria mi rentabilidad o beneficio. Si lo vendes a menos, tendrás una perdida.
- Dividendos: Algunas acciones pagan al inversor dividendos (Parte de la ganancia de una empresa se va a retribuir de forma periódica a los accionistas).
Te recomiendo que leas El poder del Interés Compuesto para que saques el mayor provecho a tu rentabilidad.
¿Cómo calculo la rentabilidad total de mi inversión?
En general, las personas cuando invierten su dinero y piensan en el retorno que les generará el mismo, lo hacen partiendo de la ganancia en términos de dinero. Mas no de la relación entre lo invertido y el beneficio, en otras palabras, de manera porcentual.
Medir la ganancia, en términos de dinero, no nos permite conocer el esfuerzo de la inversión inicial que ha producido llegar al beneficio final, por ello es necesario medirlo a nivel de porcentaje (%).
Un ejemplo:
El inversor 1 ha invertido 1.000 soles y a obtenido al final de un año 1.200 soles. Ganancia: 200 soles.
El inversor 2 ha invertido 2.500 soles y a obtenido al final de un año 2.800 soles. Ganancia: 300 soles.
Pregunta: ¿Quién ha obtenido mayor rentabilidad?
A simple vista me podrías decir que el Inversor 2 ha sido mas rentable su inversión puesto que tiene mayor ganancia, 300 soles.
Sin embargo, quien ha obtenido mayor rentabilidad o en otras palabras, quien ha obtenido mayor beneficio en relación a lo invertido es mayor del Inversor 1 que del Inversor 2.
¿Pero como es esto posible?
Pues apliquemos la formula de rentabilidad simple:
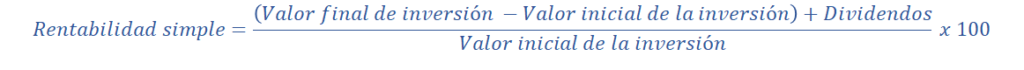
Añadimos los datos del Inversor 1:
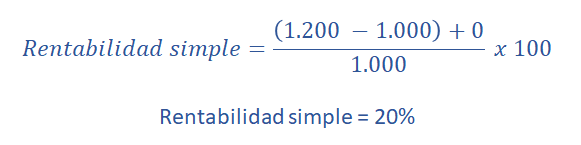
Añadimos los datos del Inversor 2:
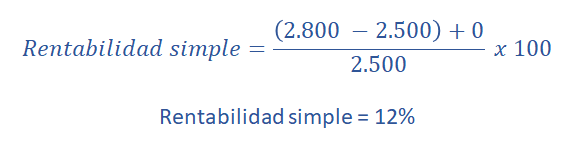
Interpretación: Existe mayor beneficio en relación con la inversión del Inversor 1; ya que ha obtenido un 20% de rentabilidad, con respecto al Inversor 2, quien ha obtenido 12% de rentabilidad en relación a su inversión.
Otro ejemplo (tomando en cuenta el ejemplo del articulo del Interés Compuesto):
Tenemos una inversión que a través de los años se va revalorizando de la siguiente manera:
| Año | Inversión |
| 0 | 1,000 |
| 1 | 1,040 |
| 2 | 1,186 |
| 3 | 1,337 |
| 4 | 1,495 |
| 5 | 1,658 |
| 6 | 1,829 |
| 7 | 2,006 |
| 8 | 2,190 |
| 9 | 2,382 |
| 10 | 2,581 |
Usando la formula de rentabilidad simple, podemos calcular la rentabilidad ya sea por el total de los 10 años o de cada año. Veámoslo a continuación:
Rentabilidad total (de los 10 años):
Añadimos los datos del año 0 (Valor inicial de la inversión) y año 10 (valor final de la inversión):
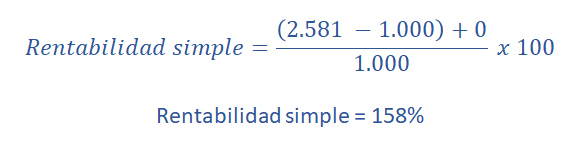
¿Cómo calculo la rentabilidad anual de mi inversión?
Si queremos saber la rentabilidad de cada año, nuevamente aplicamos la formula de la rentabilidad simple e ingresamos los datos:
Rentabilidad del año 1:
Teniendo los dato del Año 0 (Valor inicial de la inversión) y del Año 1 (valor final de la inversión), aplicamos a continuación en la formula:
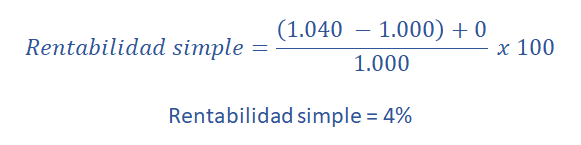
Y si replicamos año tras año, tendremos la rentabilidad de cada año, como lo vemos a continuación:
| Año | Inversión | Rentabilidad anual (%) |
| 0 | 1,000 | – |
| 1 | 1,040 | 4 |
| 2 | 1,186 | 14 |
| 3 | 1,337 | 13 |
| 4 | 1,495 | 12 |
| 5 | 1,658 | 11 |
| 6 | 1,829 | 10 |
| 7 | 2,006 | 10 |
| 8 | 2,190 | 9 |
| 9 | 2,382 | 9 |
| 10 | 2,581 | 8 |
Cuando tengas calculada la rentabilidad anualizada, es importante que apliques la formula de la rentabilidad real por cada año (rentabilidad que incluye el efecto de la inflación), para que tengas un calculo aún mas preciso: Inflación, el enemigo invisible.
¿Cómo calculo la rentabilidad acumulada de mi inversión?
En los casos que quieras calcular la rentabilidad de varios años (rentabilidad acumulada) procederemos a aplicar la misma formula de rentabilidad simple.
Veamos un par de ejemplos.
Rentabilidad acumulada en el quinto año:
Para ello aplicamos los datos del Año 0 y del Año 5; ya que queremos saber cuanto ha producido en todo ese periodo de tiempo:
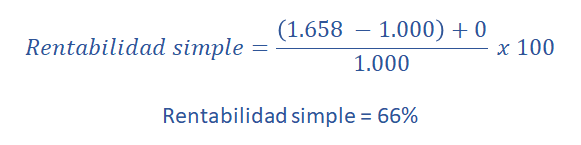
Aplicando la misma formula, calculamos la rentabilidad acumulada de los 10 años:
| Año | Inversión | Rentabilidad acumulada (%) |
| 0 | 1,000 | – |
| 1 | 1,040 | 4 |
| 2 | 1,186 | 19 |
| 3 | 1,337 | 34 |
| 4 | 1,495 | 49 |
| 5 | 1,658 | 66 |
| 6 | 1,829 | 83 |
| 7 | 2,006 | 101 |
| 8 | 2,190 | 119 |
| 9 | 2,382 | 138 |
| 10 | 2,581 | 158 |
¿Cómo calculo la rentabilidad anual de si mi inversión sube y baja?
Si mi inversión a través de los años sube y baja, así como las acciones en bolsa, no te preocupes, igual usaremos la formula de la rentabilidad simple.
Veámoslo en un ejemplo:
Una persona ha evaluado las opciones en donde invertir y ha decidido invertir 1.000 soles durante 10 años en la bolsa de valores. La volatilidad de las acciones hace que por lo general suba y bajen en valor. Al final de los 10 años veremos cuanta rentabilidad a obtenido.
| Año | Inversión |
| 0 | 1,000 |
| 1 | 980 |
| 2 | 1,200 |
| 3 | 1,124 |
| 4 | 1,345 |
| 5 | 1,658 |
| 6 | 2,035 |
| 7 | 1,923 |
| 8 | 2,431 |
| 9 | 2,512 |
| 10 | 2,650 |
Apliquemos la formula de rentabilidad simple que vimos líneas mas arriba y obtenemos los siguientes resultados:
| Año | Inversión | Rentabilidad anual (%) |
| 0 | 1,000 | – |
| 1 | 980 | -2 |
| 2 | 1,200 | 15 |
| 3 | 1,124 | -5 |
| 4 | 1,345 | 1 |
| 5 | 1,658 | 11 |
| 6 | 2,035 | 23 |
| 7 | 1,923 | 5 |
| 8 | 2,431 | 21 |
| 9 | 2,512 | 15 |
| 10 | 2,650 | 11 |
¿Por que vemos una rentabilidad de (-2%) en el primer año?
Porque el Año 0 el inversor tenia 1.000 soles; sin embargo en el Año 1 termina con menos, 980 soles.
Igualmente sucede en el Año 3, en donde obtiene una rentabilidad de (-5%).
Como ves, esta formula aplica tanto para las inversiones que tienden a subir y bajar, durante un periodo de tiempo.
¿Cómo calculo la rentabilidad media de mi inversión?
Uno de los errores cuando se calcula la rentabilidad media de nuestra inversión es hacerlo mediante el promedio aritmético. Sin embargo, lo correcto es hacerlo con el promedio geométrico.
Veámoslo por que no es correcto calcular la rentabilidad media con el promedio aritmético:
Ejemplo:
Similar a los ejemplos anteriores. Un inversor invierte 1.000 soles y al cabo del 3er año su inversión está valorizada en 900 soles:
| Año | Inversión | Rentabilidad anual (%) | ||||||||||
| 0 | 1,000 | 0 | ||||||||||
| 1 | 700 | -30 | ||||||||||
| 2 | 1,200 | 71 | ||||||||||
| 3 | 900 | -25 |
Si utilizamos el promedio aritmético (forma incorrecta) para calcular nuestra inversión, nos saldría una rentabilidad de 5.3%. Resultado de sumar las rentabilidades (-30%)+(70%)+(-25%), finalmente dividirlo entre 3.
¿Algo anda mal en esta rentabilidad media verdad? Si el inversor tenia 1.000 soles en el Año 0, y luego en el Año 3: 900 soles, ¿Cómo la rentabilidad media nos indica 5.3% y la rentabilidad total es negativa?
Pasa esto porque el promedio aritmético se usa cuando los datos son independientes uno de otro. Como por ejemplo la nota de exámenes, los cuales no dependen de la nota de los anteriores exámenes dados, sino de cuanto se ha estudiado para cada evaluación.
Es por ello que, para calcular de forma correcta la rentabilidad media, se usa el promedio geométrico.
El promedio geométrico si promedia datos que dependen unos de otros, así como los datos de nuestras inversiones. Detallado en el poder del interés compuesto.
Ahora veamos como calcular la rentabilidad media de nuestras inversión, de la forma correcta, mediante el promedio geométrico, también llamada rentabilidad anualizada.
Traemos la misma tabla de datos, anterior:
| Año | Inversión | Rentabilidad anual (%) | ||||||||||
| 0 | 1,000 | 0 | ||||||||||
| 1 | 700 | -30 | ||||||||||
| 2 | 1,200 | 71 | ||||||||||
| 3 | 900 | -25 |
- Dividimos el Valor final de la inversión entre el Valor inicial de la inversión:
(900/1.000)=0.9 - El resultado de la división lo elevamos a 1 entre el numero de años de la inversión:
0.9 ^ (1/3)=0.96 - Al resultado restamos la unidad (-1) y lo multiplicamos por cien (x100) para tener la rentabilidad media anual:
(0.96-1)*100=-3.4511%
Comprobando los métodos de promedio aritmético y promedio geométrico
Si aun así te caben dudas con respecto al método correcto de como medir la rentabilidad media de nuestra inversión, vamos a ponerlo a prueba con la formula del Interés Compuesto:
Cf=Ci(1+i)n
Donde:
Cf= Capital final
Ci= Capital inicial
i= tasa de interés
n= periodo del ahorro
Promedio aritmético: 5.3% versus Promedio geométrico: -3.4511%
Añadimos el 5.3% del promedio aritmético a la formula del Interés Compuesto:
Capital final=1.000(1+(0.053))3 = 1.167,58
Ahora, añadimos el -3.4511% del promedio geométrico a la formula del Interés Compuesto:
Capital final=1.000(1+(-0.034511))3 = 900,00
Conclusión: Mas que comprobado, si usamos la formula del Interés Compuesto vemos que la rentabilidad media que nos da el promedio geométrico es el correcto. Véase que al usar el promedio aritmético difiere en mucho, por lo que no es correcto utilizarlo.
¿Cómo calculo la rentabilidad de mi inversión con aportaciones, retiros de dinero y en cualquier fecha?
Ya si has comprendido todas las formas de obtener el calculo correcto que hemos explicado líneas arriba, ahora toca saber como calcular la rentabilidad de nuestra inversión si aporto mayor dinero, si hago retiros de dinero y si quiero saber la rentabilidad en cualquier fecha, no solamente anual.
En el mundo de la inversión a este método se le conoce como Money-Weighted Return, para resumir llamémoslo MWR.
Pareciera que fuese mas difícil. Sin embargo, es mucho mas fácil de lo que parece. Es mas, para ello vamos a utilizar una hoja de cálculo, ya sea en Excel u Google.
El MWR sirve para obtener la rentabilidad de tu dinero en el periodo que quieras (no solamente cada año), teniendo en cuenta las aportaciones y retiro de dinero que hagas, todo en un mismo calculo. Veámoslo en la practica:
Ejemplo:
Un inversor ha realizado una su primera inversión el 06.02.2020 por 10.000 soles, a continuación veamos las aportaciones, retiros:
| Fecha | Aportaciones / retiros |
| 6/02/2020 | -10,000 |
| 25/03/2020 | 500 |
| 3/06/2020 | -1,500 |
| 7/09/2020 | -300 |
| 28/10/2020 | -560 |
| 1/11/2020 | -1,600 |
| 20/02/2021 | 50 |
| 4/03/2021 | -250 |
| 20/04/2021 | 200 |
| 16/07/2021 | -1,400 |
| 25/07/2021 | 18,640 |
Siempre en la ultima fecha se tiene que colocar la inversión en positivo, a fin de que la formula calcule el monto final que se desea retirar de la inversión.
Pues bien, dicho esto vamos a calcular paso a paso la rentabilidad MWR en Excel:
- Colocar en Excel los valores tanto de Fechas y los Aportes y Retiros que se ha realizado:
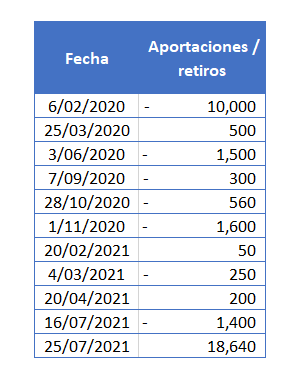
2. Al final de los valores introducimos la función «TIR.NO.PER», en VALORES señalamos los datos de «Aportaciones / retiros» y en FECHAS, las fechas de la primera columna.
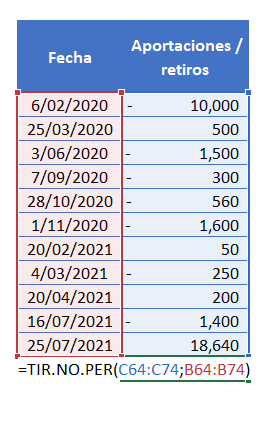
3. Luego de haber ingresado los datos a la formula «TIR.NO.PER», como resultado, nos dará 0.2072.
Podemos poner una celda abajo indicando (%) y a dicho valor de la formula lo multiplicamos por 100 para convertir el resultado a porcentaje:
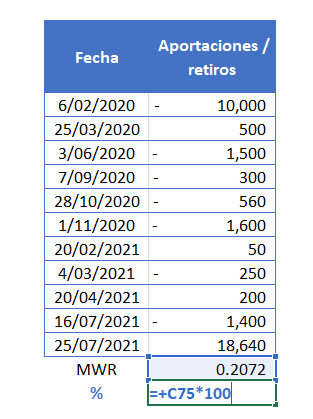
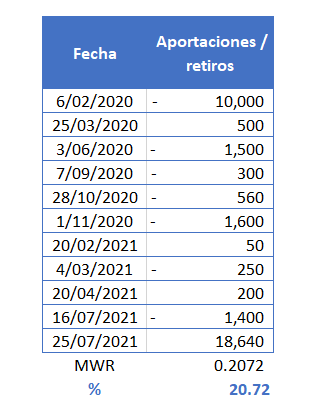
Luego de los datos de aportes y retiros de acuerdo a los diversas fechas, obtenemos una rentabilidad del 20.72%.
Si tienes alguna pregunta, sugerencia o recomendación, no dudes en dejarme un comentario más abajo.
¿te ha gustado esta entrada? ¡Compártelo en tus redes sociales!
Crédito imágenes: www.freephotos.cc


No responses yet