El poder del Interés Compuesto

“El interés compuesto es la fuerza más poderosa de la galaxia.” Albert Einstein.

¡Hola Indexados!

¿Qué es el interés compuesto?

En finanzas, el interés compuesto es el interés que produce un capital invertido en algo y que a su vez este pasa a ser capital para que sea un capital un poco mas grande y poder generar un interés aun mayor. Ello quiere decir que los intereses van a ir creciendo y como resultado tendremos un efecto de bola de nieve.

La idea es muy sencilla, sin embargo es vital comprender su potencial para aplicarlo en nuestras inversiones y sacar el verdadero poder en nuestros ganancias. Para entenderlo mejor, vamos a ver el siguiente ejemplo:

Imaginemos que vemos una publicidad de un nuevo producto bancario, nos dicen que han sacado una cuenta que nos da el 4% anual. Decidimos contratar este producto y le depositamos 1.000 soles el primer año, el cual nos daría el siguiente resultado en 10 años de 1.480 soles:

Año	Inversión	Intereses	Saldo final
1	1,000	40	1,040
2	1,040	42	1,082
3	1,082	43	1,125
4	1,125	45	1,170
5	1,170	47	1,217
6	1,217	49	1,265
7	1,265	51	1,316
8	1,316	53	1,369
9	1,369	55	1,423
10	1,423	57	1,480

Como vemos en la tabla, al principio del primer año se depositó 1.000 soles, el cual le generó 40 soles de interés (4%) al termino de ese primer año; total de 1.040 soles. Esos mismos 1.040 soles, para fines del segundo año, van a generar igualmente 4% de interés, pero ya no 40 soles, sino 42 soles.

¿Por qué si en el primer y segundo año, con el mismo porcentaje de interés, se genera 40 soles y luego 42 soles, respectivamente?

Porque en el primer año se empieza con una inversión inicial de 1.000 soles, el cual generó 40 soles, según la tasa de interés de 4%. Sin embargo, en el segundo año ya no se empieza con los 1.000 soles, sino con el interés ganado del año anterior de 40 soles, en total 1.040 soles. Estos 1.040 soles evidentemente generará 42 soles en dicho año. Asi sucesivamente en cada año, el interes ira creciendo y añadiendose al capital inicial, a lo que llamaremos el efecto de bola de nieve.

Formula del Interés Compuesto

Una manera mas practica, pero menos visual de ver el rendimiento del Interés Compuesto es usando la siguiente formula:

C_f=C_i(1+i)ⁿ
Donde:
C_f= Capital final
C_i= Capital inicial
i= tasa de interés
n= periodo del ahorro

Probemos la formula del Interés Compuesto:

Como puedes ver, el resultado es el mismo, aplicando cualquiera de los dos métodos.

¿Aun así quieres sacar mayor provecho del Interés Compuesto?

Ahora ya sabemos que cuanto mayor capital tengamos al principio de cada año, mayor será la ganancia que tendremos por el Interés Compuesto. Entonces ¿Qué pasaría si al principio de cada año añadimos 100 soles? Veámoslo a continuación:

Año	Inversión	Adicional	Intereses	Saldo final
1	1,000		40	1,040
2	1,040	100	46	1,186
3	1,186	100	51	1,337
4	1,337	100	57	1,495
5	1,495	100	64	1,658
6	1,658	100	70	1,829
7	1,829	100	77	2,006
8	2,006	100	84	2,190
9	2,190	100	92	2,382
10	2,382	100	99	2,581

Comparemos las dos tablas de Interés Compuesto. En la primera tabla dejando los 1.000 soles a 10 años al 4% terminamos con 1.480 soles. Pero si le añadimos 100 soles anuales (900 soles en total) tendremos al final 2.581 soles. ¡1.101 soles mas! A eso le llamamos tomar mayor ventaja del efecto de bola de nieve.

¿Y el Interés Simple?

Pues llamaremos al Interés Simple, al interés que no se reinvierte, en otras palabras, que no se suma al capital. Siguiendo con el ejemplo de los 1.000 soles depositados en el primer año. En vez de invertir nuevamente los 40 soles ganados, lo tenemos en «modo de pausa» sin que produzca. Veámoslo en la siguiente tabla:

Año	Inversión	Intereses	Saldo final
1	1,000	40	1,040
2	1,000	40	1,080
3	1,000	40	1,120
4	1,000	40	1,160
5	1,000	40	1,200
6	1,000	40	1,240
7	1,000	40	1,280
8	1,000	40	1,320
9	1,000	40	1,360
10	1,000	40	1,400

¡Que pasó acá!, pues el hecho de no haber reinvertido los 40 soles en el primer año hace que el siguiente año se empiece de nuevo con los 1.000 soles y así sucesivamente año tras año. Al final del periodo, obtenemos 1.400 soles, resultado de la reinversión de los 1.000 soles y los 40 soles anuales en «modo de pausa».

Interés Compuesto versus Interés Simple

Ahora, veamos una comparación grafica entre el Interés Compuesto vs Interés Simple, pero ahora usaremos un 7% anual, promedio del rendimiento histórico de la bolsa de valores en Estados Unidos (De acuerdo a Jeremy J. Siegel en su libro: Guía para invertir a largo plazo, Profit Editorial, Barcelona, 2015).

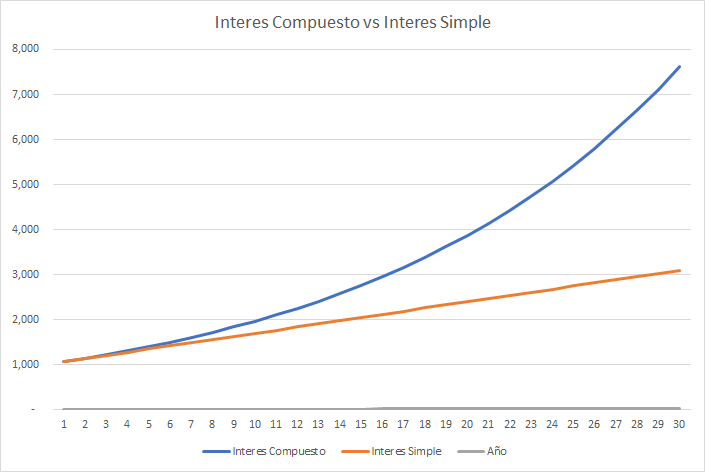
Como se aprecia en el grafico, a medida que transcurren los años, el Interés Compuesto hace uso de su efecto de bola de nieve para generan muchas mayores ganancias que el Interés Simple, ello debido a la reinversión de los intereses.

Lo que nos enseña esta grafica son cuatro factores a tomar en cuenta al invertir nuestro dinero.

• La primera, ser pacientes al momento de invertir, cada año que pasa va a generar mayores ingresos que años anteriores (efecto bola de nieve).
• El segundo, ser disciplinados reinvirtiendo los intereses, con el fin de que tu dinero trabaje para generar mayor dinero.
• Tercero, aprovecha el Interés Compuesto para aportar mensualmente montos pequeños y conseguir mas rendimiento.
• Y por ultimo, el cuarto factor, tener una estrategia solida que se adecue a nuestro estilo de vida, nivel de aprendizaje, tiempos, etc.

Si tienes alguna pregunta, sugerencia o recomendación, no dudes en dejarme un comentario más abajo.

¿te ha gustado esta entrada? ¡Compártelo en tus redes sociales!